プライバシーポリシーとサポート情報 - 統計電卓 ― 2018年09月27日 13:00
本アプリについて (About this app)
このアプリは、キーパッドから登録した数値について、平均や分散などの記述統計と、2次元データの相関および回帰の分析を行います。
※2018年9月の更新
・メニューを見直し、記述統計とヒストグラム、相関関係と散布図、への遷移をしやすくしました。
・データ一覧にタブ区切りテキストの読込ボタンを設けました。
※本アプリは、正しい結果が得られるようテストを実施し、品質確保に努めています。ただし、不具合がないことを保証するものではなく、本アプリを利用した結果生じる損害については、いかなるものについても責任を負いかねます。自己責任の範囲でご利用をお願いします。
プライバシーポリシー (Privacy statement)

対象アプリ:統計電卓
本アプリの製作者である The Fourteenth Lab (第十四工房) は、本アプリによって、お客様の個人情報およびプライバシーに関する情報を収集しません。
サポート情報 (Support)
ご質問や不具合のご連絡は、このページの「コメント欄」をご利用いただくか、「このブログについて」に記載の連絡先までお願いします。
使い方
利用方法は、アプリのメニューの「アプリの説明とプライバシーポリシー」にあります。ここでは、概略を示します。
●画面構成
縦長の画面構成を前提に説明します。
下半分)数値を入力するキーパッド、記述統計の統計量の表示部(統計量)、相関や回帰に関する統計量の表示部(相関関係)、を左右に切り替えて使用します。
上半分)入力したデータの一覧(入力データ)、ヒストグラム、散布図、を左右に切り替えて使用します。
●入力パッド

数値を入力する際、四則演算による計算ができます。最大10桁です。入力した数値、または計算結果を、「セット追加」ボタンで登録します。複数項目(変数)がある場合は、「項目追加」ボタンで登録します。
●入力データ

入力したデータを一覧形式で表示します。セット番号(行)、項目番号(列)、値、の順で表示します。データを失わないよう、適宜、保存ボタンを利用してください。リストを選択中に、編集ボタンを押すと、キーパッドの表示部の値で上書きします。
●統計量

計算対象の項目(変数)を選択すると、計算を実行します。
●ヒストグラム

「統計量」の画面で選択した項目(変数)について、ヒストグラム(柱状グラフ)を作成します。縦画面で使用する想定で、横向きです。平均値、中央値(メディアン)、平均値±2σの範囲を図示します。データの範囲が広い場合、柱の最大値を設定するボタンで、柱の数を調整できます。
●相関関係

「変数1」で独立変数、「変数2」で従属変数を選択すると、計算を実行します。
●散布図
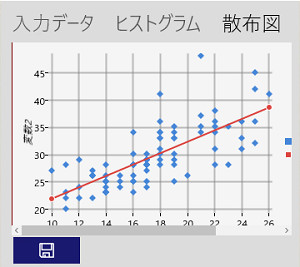
「相関関係」の画面で選択した項目(変数)を用いて、散布図を作成します。回帰直線を合わせて表示します。
●R向けスクリプト例
RGuiでの利用例を示します。
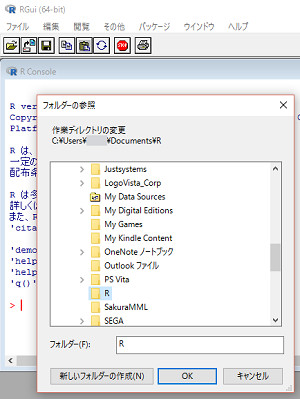
最初に、ファイルメニューから「作業ディレクトリの変更」を行い、スクリプトとデータファイルを置いているディレクトリを指定します。
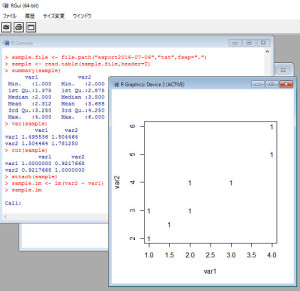
ファイルメニューから「スクリプトを開く」を選び、生成されたRスクリプトを選びます。
スクリプトが表示されたら、その上で右クリックをするとメニューが表示されます。メニューから、「全て選択」を選んだ後、「カーソル行または選択中のRコードを実行」を行います。
スクリプトが実行されます。オプションで対話型を指定しているので、クリックをするとグラフが表示されます。
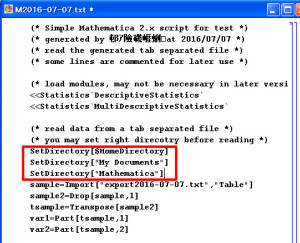
●Mathematica(4.x)向けスクリプト例
ファイルメニューの「ファイルを開く」でテキストファイルを指定し、出力したスクリプト(ファイル名の最初がMで始まる)を読み込みます。
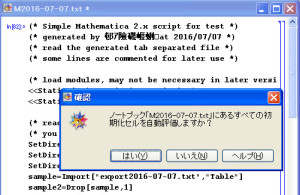
ノートブックが開くので、「SetDirectory」を適宜編集して、出力したデータファイル(タブ区切り形式)を読み込めるようにします。
なお、新しいバージョンでは、構文が変更されていますので、適宜編集してください。
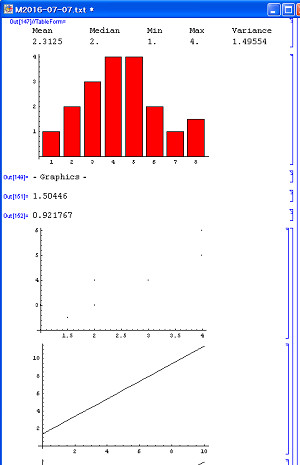
スクリプトが実行されます。入力に対応する出力を確認します。
あらかじめのおことわり (FAQ)
1)数値精度
アプリの内部では、Decimal型で管理しています。割り算では、割り切れない場合に丸め誤差が発生します。丸め方は、単純切り捨てです。四捨五入はしていません。
2)電卓部分(入力パッド)
キーボードの数字や演算キーからの入力には対応していません。
3)相関と回帰
2つの変数を選択しますが、両方の変数が揃っているセット(行)のみを対象とします。「統計量」と「相関関係」でサンプル数が異なる場合は、欠損があります。
4)散布図
・対象の数値が小数点以下の場合、軸ラベルが「0」になることがあります。
・対象変数を切り替えたとき、グラフが乱れることがあります。その場合は、一度、別のタブに切り替えてから、散布図を選択しなおすと直ります。
・サンプル数が多いと描画まで時間がかかります。機種の性能にもよりますが、300個で数秒~十数秒かかります。
5)タブ区切り形式のデータの読み込み
タイトル行など、数値以外のデータは読み飛ばします。
6)R向けスクリプト例の書き出し、Mathematica(4.x)向けスクリプト例の書き出し
おまけの扱いです。本アプリで実施できる分析に相当する機能を例示します。検算や、より詳細な分析のとっかかりにしていただく意図です。必要に応じ、編集の上、利用してください。複数項目(変数)の考慮は、変数1,変数2、の決め打ちですので、それ以外の変数は、スクリプトを編集してください。
7)グラフの出力
WinRT XAML Toolkitを使用しています。
参考文献
1)東京大学教養学部統計学教室、「基礎統計学Ⅰ 統計学入門」、東京大学出版会(1994年、第8刷)
三角形の内側判定 ― 2017年10月06日 14:07
アプリの開発中に、Polygonで描く四辺形が凹型にならないよう、移動する点が残りの3点からなる三角形の内側に入るかどうか判定しようと考えた。結局、この方法は採用しなかったが、備忘として記す。
※この目的のためには、移動する点が対角線を越えないようにすればよいのだった。
三角形の内側判定は、ゲームなどで多用されるらしく、ググってみると、ベクトルの外積を用いる方法と、3つの座標のxとyの四則演算で左回りか右回りかを判定する方法が見つかる。実装を考えると後者が簡便だが、ぱっと証明がでてこない。外積を用いる方法はエレガントだが、初等的な方法が他にないか考えてみたくなった。
P.S.
前者は重心座標を用いた方法でしょうか。
三角形の3つの頂点をx座標の小さい順にA,B,Cと名付ける。y座標の並び順の組み合わせを考えると、6つある。
調べる点が、各辺である1次直線の上にあるか、下にあるかを調べる。3辺について、上が2つ下が1つ、か、上が1つ下が2つ、の場合に、三角形の内側にありそう。bool値の積が偽で判定できる。ところが、もう少し調べてみると、この判定法では、図中の星マークの箇所で誤判定になる。
少し手直しして、x座標の2番目の頂点Bの両側の辺については同じ方向、残りの一辺についてそれとは反対の方向、にあるとする。こうすれば、正しく判定できそう。
コード的には、頂点の並び替え、一次式の導出、上下判定、と少し込み入るが、外積を求める方が軽いのかしら。
トーン系列を手頃な関数で描けないか ― 2017年01月18日 16:11
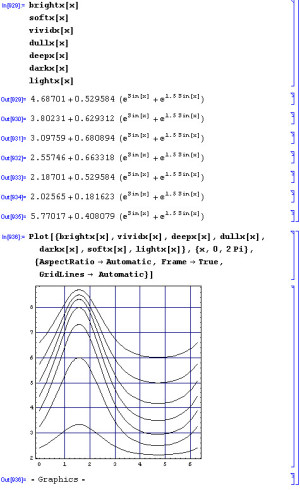
PCCS(日本色研配色体系)のトーン系列は、山が黄色(8:Y)にあり、谷が青紫(20:V)にあるような波形を描く。トーンによって、並の高さ(明度)の幅や、うねり具合が異なる。Vividは振れ幅が大きく、Deepはそれよりも小さい。参考資料を探してみたが、計算式を見つけられない。人の視覚を調査してプロットした波形で、先に式があるものではないのかもしれない。
それでも、波を描くのだから、正弦曲線でなんとかならないかとMathematicaで描いてみる。Sinを用いた式を立て、山と谷の位置で色相と明度を設定して係数をSolveで解く。山と谷の位置はあわせられるが、その途中はずれが大きい。参考資料に掲載の図を見てみると、山の尖度は大きめで、谷はゆったりした形のようだ。
そんな形の曲線はないか、と、WolframのDemonstrationのサイトを覗いてみる。Cycloidのデモが描く図形が似ている。作者は、AntiCycloidと呼んでいる。パラメータを変えて描いてみると、確かに、それらしい図形が描ける。しかし、楕円積分を実装するのは、大変そう。
要は、正弦曲線を描くときのx軸の進み方が加速減速すればいいはず。そこで、代わりに指数関数を組み合わせてみると、やや谷底がなだらかすぎる気もするが、それらしい図形になる。2項の組み合わせになったのは、試行錯誤の結果。
正弦曲線の時と同様に、それぞれのトーンについて式を立て、係数をSolveで解いてみる。正しさの保証はないが、それらしい色が出るようになった。
競走馬の誕生月と毛色 ― 2016年11月03日 14:22
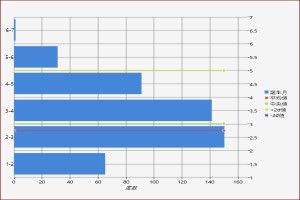
アプリの試験絡みでもう一つ。春生まれの競馬ファンは、よく自分と同じ誕生日の競走馬を見つけて応援する。実際のところ、何月生まれの馬が多いのか。2016年のセレクトセールの上場馬一覧に誕生日が掲載されていたので、ヒストグラムにする。
ラベルは、「上限-下限」で記す。下から1月生まれ、一番上が6月生まれ。2月生まれが一番多く、ついで3月生まれ。一番の遅生まれは6月。1月から4月生まれの人なら、同じ誕生日の馬を見つけられそう。
ついでに毛色も見る。アプリでは文字属性をサポートしていないので、数字に割り当てる。
鹿毛が最多。グラスワンダーの印象が残る栗毛と、黒鹿毛が次ぐ。芦毛は目立つが、少なめ。479頭の中で栃栗毛は1頭。
千葉県で住みやすいのはどこか ― 2016年11月03日 12:45
アプリの試験をかねて、千葉県内で住みやすい場所を探してみる。天候面からの検討。
急な気温の変動は体調を崩しやすいので、一年を通じて気温の変化が少なく、一日のうちの変化も少ない方がいい。気象庁の過去の気象データ・ダウンロードから、2015年の全日について、最高気温と最低気温を抜き出してみる。
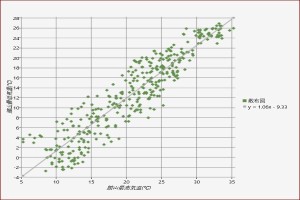
まずは、最寄りで船橋。横軸に最高気温、縦軸に最低気温をとって、全日についてプロットし、散布図を描く。強い相関が見て取れる。ここから、大まかに見て、回帰式の傾きが年間の変化の急さ、y切片の値が一日の変化の大きさを表しているといえそう。
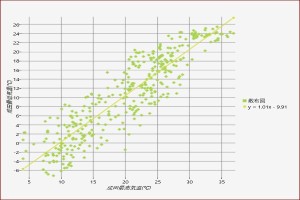
千葉県で暖かい場所というと館山が思いつく。一年を通じて温暖とのイメージだが、船橋と比べてみると、気温の幅は同じくらいだが、年間の温度変化も一日の寒暖差も少し大きい。
それならばと、ぐるっと回って、同じく海沿いの銚子。最高気温も最低気温も気温の幅は少し狭まる。年間の温度変化は館山と同じくらいだが、一日の寒暖差は少し小さい。
少し内陸に入って成田。少しばらつきは大きいが、館山に近い。寒い日は少し多め。
同じ県内なので、大同小異と言えなくもないが、今いる船橋近辺は悪くない。木更津の値も見てみるが近い。東京湾の内側の海沿いは、穏やか。同じ海に囲まれた館山と銚子なら、銚子の方が穏やか。
せっかくなので、一気に南へ。那覇。寒暖の幅がぐっと縮まる。特に低い方の気温が。年間の温度変化は船橋と同じくらいだが、一日の寒暖差はかなり小さい。
同じ暑いといっても、過ごしにくかった印象の名古屋。そんなに船橋と変わらない。過ごしやすさには、湿度の影響が大きいのか。
過ごしにくかった印象といえば京都も。夏と冬にしか行っていないけど。印象とは異なり、寒暖の幅は広めでも、年間の変化も、一日の寒暖差も小さめ。
では、暑い方の日本一。館林。年間の変化や一日の寒暖差は、穏やかな方だが、寒暖の幅、高い方にぐっと広がっている。
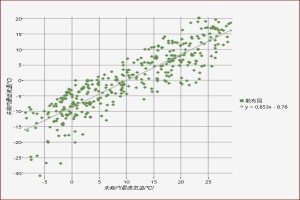
最後に、寒い方の日本一。母子里の近くの朱鞠内。寒暖の幅が低い方にぐっと寄る。一日の寒暖差も大きい方だが、なによりも最低気温の方で、回帰直線を大きく外れたいくつもの点。最高気温はいつもと変わらないが、ぐっと冷え込む日が、幾日も訪れる。
赤血球のようなものを計算で描いてみる ― 2016年10月24日 17:19
アプリのアイコンを考える内、赤血球のようなイメージなら計算で描けるのでは、と思いつく。白血球や血小板は不定形のようなので難しい。
手持ちのMathematicaのバージョンが心配だったが、以前からある関数のようで一安心。パラメータを変えていろいろ描いてみると、お饅頭というか、あんパンのようにはなる。もう一息。
それではと、トーラスの本にそれらしい図形があった気がして、Google先生に尋ねてみる。出てきたのは、カッシーニの卵形線。トーラスを上から切っていくと、穴の手前のところで、それらしい断面の図形が現れる。
極座標形式になおして、2次元で断面を描いてみる(ParametricPlot)。パラメータ(h)でくぼみ具合が決まる。
これを、Z軸を中心に回してやればと、マニュアルのサンプル(ParametricPlot3D)を手本に、よく考えずに3Dにしてみるが、回っていない。
気を取り直して、断面の描画と、回転を整理。
・2次元の時のY軸は、Z軸に
・2次元の時のX軸は、3次元では円を描くのでXとY軸に同じ値を
・Z軸を中心の回転は、回転のパラメータ(u)を使って、XとY軸に追加
できたのはこんな感じ。右手前から光を当てて、くぼみがわかりやすいように。これで、色を塗れば、それらしく見えないこともないか。
素数に憑かれた人たち リーマン予想への挑戦 ― 2016年09月24日 15:39

AmazonでWish Listを眺めていたらセール中だったので、つい。
リーマン予想を詳しく知ったのは、NHKの特集番組だったか。それまでは、非ユークリッド幾何学の人という印象だった。最近では、数理科学の2015年9月号がリーマンを特集していた。黒川さんの記事が本書の数学部分の要約になっている。Wish Listに登録したのはこの頃。ブルーバックスなどと一緒に登録している。
本書は2部構成。1部は19世紀の終わりまで。2部は20世紀以後の展開。およそ時系列に沿って進む。章立ては少し凝った造り。奇数章はどちらかというと数学の話題。偶数章は人物や時代背景を語る。面白い試みだが、問題の構造よりも時系列を優先したのは、数学の理解のしやすさを少し損なっているかも。それでも、先に読み進めさせる力はなかなか。数表やグラフも充実。
2部の18章で量子論に現れる素数の姿を少し紹介するが、あまり深入りしない。ここは少し期待していただけに残念。いろいろ脇道に逸れているようで、リーマン予想にまっすぐ進む。
初代のPaperWhiteで読んだが、イメージデータのため、ページ送りがかなり重い。字も小さめ。タブレットなら一回り大きいものがよさそう。イメージデータのため、PCのブラウザ(Kindle Cloud Reader)でも読めるのが幸い。
数学とは何か ― 2016年09月22日 11:06

学校での数学は高校までの身には、数学の本はなにかとハードルが高い。知らない記号や記法が説明なしに使われる、それらを理解するためのガイドがなかなか見つからない。数学事典、というのもあるが、これも一定ラインをクリアしていないと読みこなせない。おそらく、大学最初の頃に理系の学部生がこなす訓練の有無が大きいのだろう。
そんなこんなでいろいろな入門書を漁ってきたが、本書は、途中で詰まることなく読み進められる。序文に偽りなし。反面、文字が多くて、かなりのページ数を集中して読む必要がある。まあ、この点は、お国柄か。IT系の本でも、図表を多用する日本の教科書と異なり、米国の教科書は文字が多い。
初版は、原書が1941年(翻訳は1966年)、改訂版が1996年(翻訳は2001年)。言い回しや取り上げる例など、少し古さを感じさせないではないが、理解の支障にはならない。
章立てを示すと。
1.自然数。補足で整数論
2.数学における数系。有理数、無限、複素数、など。補足で集合の代数
3.作図法、数体の代数。
4.射影幾何学、公理論、非Euclid幾何学
5.位相幾何学
6.関数と極限。補足で極限と連続性の例題の追加
7.最大と最小
8.微分積分学。補足で微分可能性、大きさの位数、ゼータ関数など
9.最近の発展。改訂版で追加されたもの
個人的には、コンパクトな集合、微分方程式、指数関数の重要性、ゼータ関数、あたりの説明が収穫。終章でのFermatの最終定理の説明も4ページほどと短いが、解明に至る構造をこれまでで一番明確に示したもの。


















最近のコメント